LOG#118. Basic Neutrinology(III).
Posted: 2013/07/13 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: Dirac mass term, GUT baryon-lepton mass models, GUTs, LR models, magnetic dipole moments, Majorana fermion, Majorana mass term, mass terms, neutrinology, New Physics, pseudo-Dirac fermion, seesaw, seesaw limit, seesaw types, singlet mass term, SO(10), triplet mass term |Leave a commentMass terms
Phenomenologically, lagrangian mass terms can be understood as terms describing “transitions” between right (R) and left (L) handed states in the electroweak sector. For a given minimal, Lorentz invariant set of 4 fields (), we have the components of a generic Dirac spinor. Thus, the most general mass part of a (likely extended) electroweak massive lagrangian can be written as follows:
In terms of a “new” Majorana (real) field with and
, we have
and then, the massive lagrangian becomes
where the neutrino mass matrix is defined to be
We can diagonalize this mass matrix and then we will find the physical particle content! It is given (in general) by two Majorana mass eigenstates: the inclusion of the Majorana mass splits the 4 degenerate states of the Dirac field into two non-degenerate Majorana pairs. If we assume that the states are respectively “active” (i.e., they belong to some weak doublets) and sterile (weak singlets), then the terms corresponding to the Majorana masses
transform as weak triplets and singlets respectively. While the term corresponding to
is an standard, weak singlet in most cases, Dirac mass term, its pressence shows to be essential in the next discussion. Indeed, this simple example can be easily generalized to three or more families, in which case the masses beocme matrices themselves. The complete full flavor mixing comes from any two different parts: the diagonalization of the charged lepton Yukawa couplings and that of the neutrino masses! Most of beyond Standard Model theories (specially those coming from GUTs) produce CKM-like leptonic mixing and this mixing is generally “arbitrary” with parameters only to be determined by the experiment. Only when you have an additional gauge symmetry (or some extra discrete symmetry), you can guess some of the mixing parameters from first principles. Therefore, the prediction of the neutrino oscillation/mixing parameters, as for the quark hierarchies and mixing, need further theoretical assumptions NOT included in the Standard Model. For instance, we could require that the
mixing were “maximal” or to impose some “permutation symmetry” and derive the neutrino oscillation parameters from “tribimaximal” or “trimaximal” mixing. However, currently, the symmetry behind the neutrino mass matrix or the quark mixing matrix (the CKM mass matrix) are completely unknown. We can feel and “smell” there are some patterns there (something that suggests a “new” approximate broken symmetry related to flavor) but there is no current accepted working model for the neutrino mass matrix (or its quark analogue, the CKM mass matrix).
The seesaw
When we diagonalize the above neutrino mass matrix, we can analyze different “limit” cases. In the case of a purely Dirac mass term, i.e., whenver , then the
states are degenerate with mass
and a four component Dirac field can be “recovered” as
, modulo some constant prefactor. It can be seen that, although violating individual lepton numbers, the Dirac mass term allows a conserve dlepton number
. This case in which the triplet and scalar masses are “tiny” or, equivalently, the case in which their Majorana mass “separation” is very small is sometimes called “pseudo-Dirac” case. In fact, it produces some interesting models both in Cosmology and particle physics. Inded, it could be possible that the 3 neutrino flavors we do know today were, in fact, neutrino (almost degenerated) triplets, i.e., every neutrino flavor could be formed by 3 very close Majorana states that we can not “resolve” using current technology.
In the general case, pure Majorana mass transition terms () arise in the lagrangian. Therefore, particle-antiparticle transitions violating the total lepton number by two units do appear (
). They can be understood as the creation or annihilation of two neutrinos, and thus, they allow the possibility of the existence of neutrinoless double beta decays! That is, only when the neutrino is a Majorana particle, the channel in which the total lepton number is violated opens.
When every mass term is allowed, there is an interesting case commonly referred as “the seesaw” limit. In this limit, taking the triplet mass to be zero and the singlet mass to be “huge” or “superheavy”, we deduce that
with
(the “seesaw” limit).
In this seesaw limit, the neutrino mass matrix can be diagonalized and it provides two eigenvalues:
Thus, the seesaw mechanism provide a way in which we obtain two VERY different mass eigenstates, i.e., two single particle states separated by a huge mass hierarchy! There is one (super)heavy neutrino (generally speaking, it corresponds to the right-handed neutrino) and a much lighter neutrino state, one that can be made relatively much lighter than a normal Dirac fermion mass. One fo the neutrino mass is “suppressed” and balanced up (hence the name “seesaw”) by the (super)heavy species. The seesaw mechanism is a “natural” way of generating two different (often VERY separated) mass scales!
The theory of the seesaw mechanism is very rich. I will not discuss its full potential here. There are 3 main types of seesaw mechanisms (generally named as type I, type II and type III) and some other less frequent variants and subvariants…It is an advanced topic for a whole future thread! 😉 However, I will draw you the 3 main Feynman graphs involved in these 3 main types of seesaw mechanisms:
GUTs and neutrino mass models
Any fully satisfactory model that generates neutrino masses must contain a natural mechanism which allows us to explain their samll value, relative to that of their charged partners. Given the latest experimental hints and results, it would also be possible that it will include any comprehensive explanation for light sterile neutrinos and large, nearl maximal, mixing. This last idea is due to some “anomalies” coming from some neutrino experiments (specially those coming from reactors and the celebrated LSND experiment).
Different models can be distinguished according to the new particle content and spectrum, or according to the energy scale hierarchy they produce. With an extended particle content, different options open: if we want to brak the lepton number ant to generate neutrino masses without introducing new (unobserved) fermions in the SM, we must do it by adding to the SM Higgs sector fields carrying lepton numbers. Thus, one can arrange them to break the lepton number explicitly or spontaneously through interactions with these fields. If you want, this is another reason why the Higgs field matters: it allows to introduce fields carrying lepton numbers without adding any extra fermion field! Likely, the most straightforward approach to generate neutrino masses is to introduce for each neutrino an additional weak neutral single (that can be identified with the right-handed neutrino we can not observed due to be “very massive” and/or uncharged under the SM gauge group). This last fact strongly favors seesaw-like models!
For instance, the above features happen in the framework of LR (Left-Right) symmetric models in Grand Unified Theories (GUTs). There, the origin of the SM parity violation (explicit in the electroweak and weak sectors) is due to the spontaneous symmetry breaking of a baryon-lepton symmetry, and it yields a quantum number conservation/violation up to a degree that depends on the particular model. Thus, in
GUT, the Majorana neutral particle N enters in a natural way in order to complete the matter multiplet. Therefore, N should be a
singlet, as we wished it to be.
If we use the energy scale as a guide where the new physics have relevant effects, unification (e.g., think about the previous SO(10) example) and the weak scale approach (radiative models and their effective theories) are usually distinguished and preferred form a pure QFT approach.
Despite the fact that the explanation of the known neutrino anomalies (the solar neutrino problem the first, but also the atmospheric neutrino flux and the reactor anomalies/neutrino beam anomalies) do not need or require the existence of an additional extra light/heavy sterile neutrino, some authors claim that they could exist after all. If every Marojana mass term is “small enough”, then active neutrinos can oscillate or mix into sterile (likely right-handed) fields/states. Light sterile neutrinos can appear in particularly special see-saw mechanisms if additional assumptions are considered (there, some models called “singular seesaw” models do exist as well). with some inevitable amount of “fine tuning”. The alternative to “fine tuning” would be seesaw-like suppression for sterile neutrinos involving new unknown (likely ultraweak or “dark”) interactions, i.e., family symmetries resulting in substantial field additions to the SM (some string theory models also suggest this possibility).
There is also weak scale models, i.e., radiative generated mass models where the neutrino masses are zero at tree level and they constitute a very different type of models: they explain the smallness of the neutrino masses a priori for both active and sterile neutrinos. Loop corrections induce neutrino mass terms in these models. Thus, different mass scales are generated naturally by the different number of loops involved in the generation of each term. The actual implementation requires, however, the ad hoc (a posteriori) introduction of new Higgs particles with non-standard electroweak quantum numbers and lepton number violating couplings. This is the price we pay in an alternative approach.
The origin of the different Dirac and Majorana mass terms appearing in the neutrino (seesaw like) neutrino mass matrix is usually understood by a dynamical mechanism where at some energy scale it happens “naturally” and/or where some symmetry principle is spontaneously broke and invoked. Firstly, we face with the Dirac mass term. In one special case,
and
are SU(2) doublets and singlets respectively. The mass term describes a
transition and it is generate from the SU(2) breaking via a Yukawa coupling:
Here, are the components of certain Higgs doublet. The coefficients
are the Yukawa couplings. After symmetry breaking,
, where
is the vacuum expectation value of the Higgs doublet. A Dirac mass term is qualitatively just like any other fermion mass, but that leads to the question of why it is so small in comparison with the rest of fermion masses: one would require
in order to have
. In other words,
while for the hadronic sector we have
. In principle, it could be that there is no reason beyond the fine tuning of the Yukawa couplings (via Higgs vacuum expectation values to different fields) but, as much as large hierarchies or dimensionless ratios appear, it demands “an explanation”.
In the case of the Majorana mass term, the term will appear if
is a gauge singlet on general grounds. In this case, a renormalizable mass term with structure
is allowed by the SM gauge group. However, it would bot be consistent in general with unified symmetries or general GUTs. That is, a full SO(10), for instance, and some complicated mechanisms should be used to describe and explain the presence of this term. The term is usually associated with the breaking of some larger symmetry group, and it is generally expected that its energy scale should be in a range covering from the few hundreds of
in LR models to GUTscale energies, or about
GeV.
When the term is present, then
are active. That is, whenever
is active, there is a
term. It belongs to some gauge doublet and it sometimes introduce non-renormalizable interactions. That is the reason why generally speaking models with
are “preferred” over this alternative. In this case, we have
and
must be generated by either:
1) An elementary Higgs triplet.
2) An effective operator involving two Higgs doublets arranged to transform as a triplet.
In both cases, we can induce non-renormalizable interactions. In case 1), an elementary triplet , where
is a Yukawa coupling and
the triplet v.e.v. The simplest realization is the so-called “old Gelmini-Roncadelli model”) and it is EXCLUDED by the LEP data on the Z-invisible width. This last result is due to the fact that the corresponding Majoron particle couples to the Z boson, and it increases significantly its width so we would have seen it at LEP. Some variants of this model involving the explicit lepton number violation or in which the Majoron is mainly a weak singlet (named invisible Majoron models) could still be possible, though, yet. In case 2), for an effective operator originated mass, one should expect
, where
is the scale of new physics wich generates the operator. Let me remark that both cases can trigger non-renormalizability in the extended gauge theory, a property which some people finds “disturbing”.
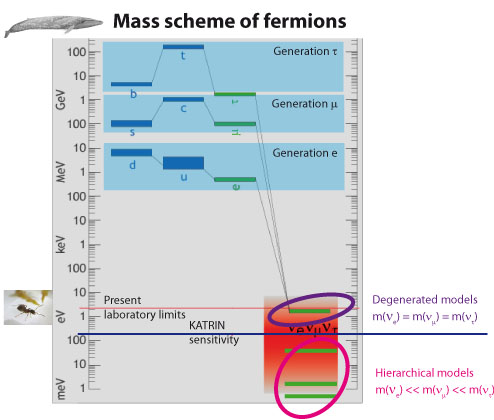
Final remarks: If (typical in LR models), and with typical values of
, one would expect masses about
for the
weak eigenstates, respectively. GUT theories motivates a bigger gap between the intermediate electroweak scale and the GUT scale. The gap can be as large as
. In the lower end of this range, for
, we have some string-inspired models, GUT with multiple breaking stages and “mixed” models. At the upper end, for
(named GUT seesaw, with large Higgs representations), one typically finds smaller masses for the neutrinos, about
eV respectively for the 3 neutrino flavors (electron, muon and tau). Somehow, this radical approach is more difficult to fit into the present known experimental facts, that they suggest a milielectronvolt neutrino mass as the lighter neutrino mass, up to 1eV (if you consider some experiments as hinting a sterile neutrino as “yet possible”). Thus, neutrinos are hinting to the existence of some intermediate pre-GUT or GUT-like unification energy scale. Where is it? We don’t know! There are many possible models and theories GUT-like. For instance, the next scheme is possible
Neutrinos and magnetic dipole moments
The magnetic dipole moment is another probe of possible new interactions and physics beyond the Standard Model. Majorana neutrinos have identically zero magnetic and electric dipole moments. Flavor transition magnetic moments are allowed however in general for both Dirac and Majorana neutrinos! Limits obtained from laboratory experiments (LEX) are of the order of a constant times , where
is the Bohr magneton. There are additional limits/bounds imposed by both stellar physics (or astrophysics) and cosmology in the range
. In the SM, the electroweak sector can be extended to allow for Dirac neutrino masses, so that the nuetrino magnetid ipole moment is nonzero and given by
The proportionality of to the neutrino mass is due to the absence of an interaction with
in this Dirac extended SM. Then, only its Yukawa coupling appears, and hence, the neutrino mass. In LR symmetric theories (like the mentioned SO(10) theory), the
is proportional to the charged lepton mass. Based on general grounds, we find typical values about
These values are still too small to have odds of being measurable in current experiments or having practical astrophysical or cosmological consequences we could detect now. However, these magnetic dipole moments are important features of BSM models, so it is important to study them.
Magnetic moment interactions arise in ANY renormalizable gauge theory only as finite radiative corrections. The diagrams which generate a magnetic moment will also contribute to the neutrino mass once the external photon line is removed.In the absence of additional symmetries, a large magnetic moment is incompatible with a small neutrino mass. The way out to this NO-GO theorem suggested by Voloshin consists in defining a symmetry acting on the flavor space
, and then the magnetic moment term are singlets under this symmetry. In the limit of exact
symmetry, the neutrino mass is forbidden BUT the magnetic moment
is allowed. Diverse concrete models have been proposed where such extra symmetry is embedded into an extension of the SM (e.g., in LR models, with SUSY “horizontal” gauge symmetries, by Babu et al.).
What do you think? Some novel idea? Here you are a decision tree map (LOL):
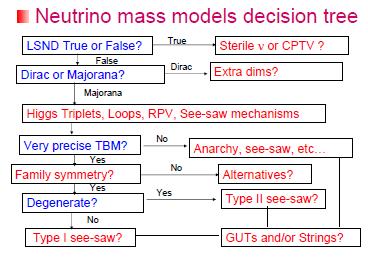 However, we are far, far away to understand the neutrino hidden higher secrets! Here you are a basic “road map” towards superbeams and neutrino factories, yet an intermediate step before the mythical muon collider (yes, USA likely WANTS that muon collider, :P)…
However, we are far, far away to understand the neutrino hidden higher secrets! Here you are a basic “road map” towards superbeams and neutrino factories, yet an intermediate step before the mythical muon collider (yes, USA likely WANTS that muon collider, :P)…
 May the neutrinos be with you!
May the neutrinos be with you!
PS: See you in my next neutrinology blog post!







You must be logged in to post a comment.