WARNING: UPGRADED TSOR website!

Posted: 2013/08/13 | Author: amarashiki | Filed under: Physmatics, Uncategorized | Tags: Physmatics, polls, TSOR, upgrade | 2 Comments

Hi there! I am Amarashiki (a new “doctor” project). And I have a new upgraded The Spectrum Of Riemannium website!

I will keep this free site though, as backup material. But everything has been moved to the new URL: http://thespectrumofriemannium.com

ALERT: If you was reading my stuff via e-mail, RSS or any other magic device/too, upgrade my URL, please. I will NOT post here anymore. After all, I am paying for the new domain! And it brings new abilities or superpowers to my web! 🙂

I wish you will enjoy my new (improved) site, since even when this beginning trip has ended, a new one is coming! And I hope It will be satisfactory for all of us!

I will be happy to hear from any other suggestion or idea related to my site! Any desiderata? XD

TSOR is just beginning!!!!!!!!

FINAL POLLS

LOG#127. Basic Neutrinology(XII).

Posted: 2013/07/22 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics | Tags: electron density, mass eigenstates, matter density, MSW effect, neutrino mixing, neutrino oscillations, neutrino oscillations in matter, neutrino oscillatrions in vacuum, neutrino refraction, neutrinology, refraction, resonance, weak eigenstates | Leave a comment

When neutrinos pass through matter or they propagate in a medium (not in the vacuum), a subtle and potentially important effect occurs. This is called the MSW effect (Mikheyev-Smirnov-Wolfenstein effect). It is pretty similar to a refraction of light in a medium, but now it happens that the particle (wave) propagating are not electromagnetic waves (photons) but neutrinos! In fact, the MSW effect consists in two different effects:

1st. A “resonance” enhancement of the neutrino oscillation pattern.

2nd. An adiabatic (i.e. slow) or partially adiabatic neutrino conversion (mixing).

In the presence of matter, the neutrino experiences scattering and absorption. This last phenomenon is always negligible (or almost in most cases). At very low energies, coherent elastic forward scattering is the most important process. Similarly to optics, the net effect is the appearance of a phase difference, a refractive index or, equivalently, a neutrino effective mass.

The neutrino effective mass can cause an important change in the neutrino oscillation pattern, depending on the densities and composition of the medium. It also depends on the nature of the neutrino (its energy, its type and its oscillation length). In the neutrino case, the medium is “flavor-dispersive”: the matter is usually non-symmetric with respect to the lepton numbers! Then, the effective neutrino mass is different for the different weak eigenstates!

I will try to explain it as simple as possible here. For instance, take the solar electron plasma. The electrons in the solar medium have charged current interactions with $\nu_e$ but not with $\nu_\mu, \nu_\tau$ . Thus, the resulting interaction energy is given by a interaction hamiltonian

(1) $H_{int}=\sqrt{2}G_FN_e$

where the numerical prefactor is conventional, $G_F$ is the Fermi constant and $N_e$ is the electron density. The corresponding neutral current interactions are identical fo al the neutrino species and, therefore, we have no net effect on their propagation. Hypothetical sterile neutrinos would have no interaction at all either. The effective global hamiltonian in flacor space is now the sum of two terms, the vacuum hamiltonian and the interaction part. We can write them together

(2) $H_w^{eff}=H_w^{eff,vac}+H_{int}\begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{pmatrix}$

The consequence of this new effective hamiltonian is that the oscillation probabilities of the neutrino in matter can be largely increased due to a resonance with matter. In matter, for the simplest case with 2 flavors and 2 dimensions, we can define an effective oscillation/mixing angle as

(3) $\boxed{\sin\theta_M=\dfrac{\sin 2\theta/L_{osc}}{\left[\left(\cos 2\theta/L_{osc}-G_FN_e/\sqrt{2}\right)^2+\left(\sin 2\theta/L_{osc}\right)^2\right]^{1/2}}}$

The presence of the term proportional to the electron density can produce “a resonance” nullifying the denominator. there is a critical density $N_c^{osc}$ such as

(3) $\boxed{N_c^{osc}=\dfrac{\Delta m^2\cos 2\theta}{2\sqrt{2}EG_F}}$

for which the matter mixing angle $\theta_M$ becomes maximal and $\sin 2\theta_M\longrightarrow 1$ , irrespectively of the value of the mixing angle in vacuum $\theta$ . The probability that $\nu_e$ oscillates or mixes into a $\nu_\mu$ weak eigenstate after traveling a distance $L$ in this medium is give by the vacuum oscillation formula modified as follows:

1st. $\sin 2\theta\longrightarrow \sin 2\theta_M$

2nd. The kinematical factor differs by the replacement of $\Delta m^2$ with $\Delta m^2\sin 2\theta$ . Hence, it follows that, at the critical density, we have the oscillation probability in matter (2 flavor and 2 dimensions):

(4) $\boxed{P_m (\nu_e\longrightarrow \nu_\mu;L)_{N_e=N_c^{osc}}=\sin^2\left(\sin 2\theta \dfrac{L}{L_{osc}}\right)}$

This equation tells us that we can get a full conversion of electron neutrino weak eigenstates into muon weak eigenstates, provided that the length and energy of the neutrino satisfy the condition

$\sin 2\theta \dfrac{L}{L_{osc}}=\dfrac{n\pi}{2}$ $\forall n=1,2,3,\ldots,\infty$

There is a second interesting limit that is mentioned often. This limit happens whenever the electron density $N_e$ is so large such that $\sin 2\theta_M\longrightarrow 0$ , or equivalently, $\theta_M\longrightarrow \pi/2$ . In this (dense matter) limit, there are NO oscillation in matter (they are “density suppresed”) because $\sin 2\theta_M$ vanishes and we have

$P_m (\nu_e\longrightarrow \nu_\mu;L)_{\left(N_e>>\dfrac{\Delta m^2}{2\sqrt{2}EG_F}\right)}\longrightarrow 0$

Therefore, the lesson here is that a big density can spoil the phenomenon of neutrino oscillations!

In summary, we have learned here that:

1st. There are neutrino oscillations “triggered” by matter. Matter can enhance or enlarge neutrino mixing by “resonance”.

2nd. A high enough matter density can spoil the neutrino mixing (the complementary effect to the previous one).

The MSW effect is particularly important in the field of geoneutrinos and when the neutrinos pass through the Earth core or mantle, as much as it also matters inside the stars or in collapsing stars that will become into supernovae. The flavor of neutrino states follows changes in the matter density!

See you in my next neutrinological post!

LOG#126. Basic Neutrinology(XI).

Posted: 2013/07/22 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: IceCube, LBE, long baseline experiments, neutrino beam experiments, neutrino masses and lepton asymmetry, neutrino mixing, neutrino oscillation experiments, neutrino oscillations, neutrino oscillations in matter, neutrino oscillations in vacuum, neutrino telescopes, neutrinology, NOCILLA, NOSEX, reactor experiments, right-handed neutrinos, SBE, short baseline experiments, sterile neutrinos | Leave a comment

Why is the case of massive neutrinos so relevant in contemporary physics? The full answer to this question would be very long. In fact, I am making this long thread about neutrinology in order you understand it a little bit. If neutrinos do have nonzero masses, then, due to the basic postulates of the quantum theory there will be in a “linear combination” or “mixing” among all the possible “states”. It also happens with quarks! This mixing will be observable even at macroscopic distances from the production point or source and it has very important practical consequences ONLY if the difference of the neutrino masses squared are very small. Mathematically speaking $\Delta m_{ij}^2=m_i^2-m_j^2$ . Typically, $\Delta m_{ij}\leq 1eV$ , but some “subtle details” can increae this upper bound up to the keV scale (in the case of sterile or right-handed neutrinos, undetected till now).

In the presence of neutrino masses, the so-called “weak eigenstates” are different to “mass eigenstates”. There is a “transformation” or “mixing”/”oscillation” between them. This phenomenon is described by some unitary matrix U. The idea is:

$\mbox{Neutrino masses}\neq 0\longrightarrow \mbox{Transitions between neutrino mass eigenstates}$

$\mbox{Transitions between mass eigenstates}\longrightarrow \mbox{Neutrino mixing matrix}$

$\mbox{Neutrino mixing matrix}\longrightarrow \mbox{Neutrino oscillations}$

If neutrinos can only be created and detected as a result of weak processes, at origin (or any arbitrary point) we have a weak eigenstate as a “rotation” of a mass eigenstate through the mixing matrix U:

$\boxed{\vert \nu_w (0)\rangle =U\vert \nu_m (0)\rangle}$

In this post, I am only to introduce the elementary theory of neutrino oscillations (NO or NOCILLA)/neutrino mixing (NOMIX) from a purely heuristic viewpoint. I will be using natural units with $\hbar=c=1$ .

If we ignore the effects of the neutrino spin, after some time the system will evolve into the next state (recall we use elementary hamiltonian evolution from quantum mechanics here):

$\vert \nu_m (t)\rangle=\exp \left( -iHt\right)\vert \nu_m (t)\rangle$

and where $H$ is the free hamiltonian of the system, i.e., in vacuum. It will be characterized by certain eigenvalues

$H=\mbox{diag}(\ldots,E_i,\ldots)$

and here, using special relativity, we write $E_i^2=p_i^2+m_i^2$

In most of the interesting cases (when $E\sim MeV$ and $m\sim eV$ ), this relativistic dispersion relationship $E=E(p,m)$ can be approximated by the next expression (it is the celebrated “ultra-relativistic” approximation):

$p\simeq E$

$E\simeq p+\dfrac{m^2}{2p}$

The effective neutrino hamiltonian can be written as

$H_{eff}=\mbox{diag}(\ldots,m_i^2,\ldots)/2E$

and

$\vert \nu_m (t)\rangle=U\exp \left(-iH_{eff}t\right)U^+\vert \nu_w (0)\rangle=\exp \left(-iH_w^{eff}t\right)\vert \nu_m (0)\rangle$

In this last equation, we write

$H_w^{eff}\equiv \simeq \dfrac{M^2}{2E}$

with

$M\equiv U\mbox{diag}\left(\ldots,m_i^2,\ldots\right)U^+$

We can perform this derivation in a more rigorous mathematical structure, but I am not going to do it here today. The resulting theory of neutrino mixing and neutrino oscillations (NO) has a beautiful corresponded with Neutrino OScillation EXperiments (NOSEX). These experiments are usually analyzed under the simplest assumption of two flavor mixing, or equivalently, under the perspective of neutrino oscillations with 2 simple neutrino species we can understand this process better. In such a case, the neutrino mixing matrix U becomes a simple 2-dimensional orthogonal rotation matrix depending on a single parameter $\theta$ , the oscillation angle. If we repeat all the computations above in this simple case, we find that the probability that a weak interaction eigenstate neutrino $\vert \nu_w\rangle$ has oscillated to other weak interaction eigenstate, say $\vert \nu_w'\rangle$ when the neutrino travels some distance $l=ct$ (remember we are supposing the neutrino are “almost” massless, so they move very close to the speed of light) is, taking $\nu_m=\nu_e$ and $\nu_m'=\nu_\mu$ ,

(1) $\boxed{P(\nu_e\longrightarrow \nu_\mu;l)=\sin^22\theta\sin^2\left(\dfrac{l}{l_{osc}}\right)}$

This important formula describes the probability of NO in the 2-flavor case. It is a very important and useful result! There, we have defined the oscillation length as

$\dfrac{1}{l_{osc}}\equiv\dfrac{\Delta m^2 l}{4E}$

with $\Delta m^2=m_1^2-m_2^2$ . In practical units, we have

(2) $\boxed{\dfrac{1}{l_{osc}}=\dfrac{\Delta m^2 l}{4E}\simeq 1.27\dfrac{\Delta m^2(eV^2)l(m)}{E(MeV)}=1.27\dfrac{\Delta m^2(eV^2)l(km)}{E(GeV)}}$

As you can observe, the probabilities depend on two factors: the mixing (oscillation) angle and the kinematical factor as a function of the traveled distance, the momentum of the neutrinos and the mass difference between the two species. If this mass difference were probed to be non-existent, the phenomenon of the neutrino oscillation would not be possible (it would have 0 probability!). To observe the neutrino oscillation, we have to make (observe) neutrinos in which some of this parameters are “big”, so the probability is significant. Interestingly, we can have different kind of neutrino oscillation experiments according to how large are these parameters. Namely:

–Long baseline experiments (LBE). This class of NOSEX happen whenever you have an oscillation length of order $l\sim 10^{2}km$ or bigger. Even, the neutrino oscillations of solar neutrinos (neutrinos emitted by the sun) and other astrophysical sources can also be understood as one of this. Neutrino beam experiments belong to this category as well.

-Short baseline experiments (SBE). This class of NOSEX happen whenever the distances than neutrino travel are lesser than hundreds of kilometers, perhaps some. Of course, the issue is conventional. Reactor experiments like KamLAND in Japan (Daya Bay in China, or RENO in South Korea) are experiments of this type.

Moreover, beyond reactor experiments, you also have neutrino beam experiments (T2K, $NO\nu A$ , OPERA,…). Neutrino telescopes or detectors like IceCube are the next generation of neutrino “observers” after SuperKamiokande (SuperKamiokande will become HyperKamiokande in the near future, stay tuned!).

In summary, the phenomenon of neutrino mixing/neutrino oscillations/changing neutrino flavor transforms the neutrino in a very special particle under quantum and relativistic theories. Neutrinos are one of the best tools or probes to study matter since they only interact under weak interactions and gravity! Therefore, neutrinos are a powerful “laboratory” in which we can test or search for new physics (The fact that neutrinos are massive is, said this, a proof of new physics beyond the SM since the SM neutrinos are massless!). Indeed, the phenomenon is purely quantum and (special) relativist since the neutrinos are tiny particles and “very fast”. We have seen what are the main ideas behind this phenomenon and the main classes of neutrino experiments (long baseline and shortbaseline experiments). Moreover, we also have “passive” neutrino detectors like SuperKamiokande, IceCube and many others I will not quote here. They study the neutrino oscillations detecting atmospheric neutrinos (the result of cosmic rays hitting the atmosphere), solar neutrinos and other astrophysical sources of neutrinos (like supernovae!). I have talked you about cosmic relic neutrinos too in the previous post. Aren’t you convinced that neutrinos are cool? They are “metamorphic”, they have flavor, they are everywhere!

See you in my next neutrinological post!

LOG#125. Basic Neutrinology(X).

Posted: 2013/07/17 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: 5 sigma, CMB, CNB, cosmic ray, cosmic rays and physics, cross-section, delta particle, delta resonance, Greisen–Zatsepin–Kuzmin limit, GZK cut-off, GZK effect, H-burst, H-dip, neutrino astronomy, neutrino cosmology, neutrino spectroscopy, neutrinology, resonance, X-burst, X-dip, Z-burst, Z-dip, Zetta-electron-volt, ZeV, Zevatron | Leave a comment

The topic today is a fascinant subject in Neutrino Astronomy/Astrophysics/Cosmology. I have talked you in this thread about the cosmic neutrino background ( $C\nu B$ ) and that the young neutrino Astronomy or neutrino telescopes will become more and more important in the future. The reasons are simple:

1st. If we want to study the early Universe, we need some “new” tool to overcome the last scattering surface as a consequence of the Cosmic Microwave Background (CMB). Neutrinos are such a new tool/probe! They only interact weakly with matter and we suspect that there are some important pieces of information related to the quark and lepton “complementarity” hidden in their mixing parameters.

2nd. Due to the GZK effect, we expect that the flux of cosmic rays will suffer a sudden cut-off at about $5\cdot 10^{19}eV=50\cdot 10^{18}eV=50EeV$ , or about 8 joules. This Greisen–Zatsepin–Kuzmin limit (GZK limit) is a theoretical upper limit on the energy of cosmic rays, since at some high energy, that can be computed, they would interact with the CMB photons producing a delta particle ( $\Delta$ ) which would spoil the observed cosmic rays flux as its decays would not be detected after “a long trip”. Then, it can only be approached when the cosmic rays travel very long distances (hundreds of million light-years or more). Here you are a typical picture of SuperKamiokande cosmic ray detection:

The limit is at the same order of magnitude as the upper limit for energy at which cosmic rays have experimentally been detected. There are some current experiments that “claim” to have observed this GZK effect, but evidence is not conclusive yet as far as I know. Some experiments claim (circa 2013, July) to have observed it, other experiments claim to have observed events well above the GZK limit. The next generation of cosmic ray experiments will confirm this limit from SM physics or they will show us interesting new physics events!

Inspired by the GZK effect, some people have suggested an indirect way to detect the existence of the cosmic relic neutrinos. Remember, cosmic neutrinos have a temperature about $1.9K$ if the SM is right, and their associated neutrino density now is about $110$ per cubic centimeter per species (neutrino plus antineutrino), or $330$ per cubic centimeter including the 3 flavors! Relic neutrinos are almost everywhere, but they are very, very feeble (neutral and weakly interacting) particles. While detecting the $C\nu B$ temperature is one of the most challenging tests of the standard cosmological model, we can try to detect the existence of these phantom neutrinos using a similar (quantum) trick than the one used in the GZK limit (there the delta particle resonance). If some ultra high energy cosmic ray (likely a neutrino coming from some astrophysical source) hits a “relic neutrino” with energy high enough to produce, say, a Z boson (neutral particle as the neutrino himself), then we should observe a “dip” in the cosmic ray spectrum corresponding to this “Z-burst” event! This mechanism is also called the ZeVatron or the Z-dip. It also shows the deep links between particle physics and Cosmology or Astrophysics. When an ultra-high energy cosmic neutrino collides with a relic anti-neutrino in our galaxy and annihilates to hadrons, this process proceeds via a (virtual) Z-boson:

$\nu_{UHE}+\bar{\nu}_{C\nu B}\longrightarrow Z\longrightarrow \mbox{hadrons}$

The cross section for this process becomes large if the center of mass energy of the neutrino-antineutrino pair is equal to the Z-boson mass (such a peak in the cross section is what we call “resonance” in High Energy physics). Assuming that the relic anti-neutrino is at rest, the energy of the incident cosmic neutrino has to be the quantity:

$\boxed{E_{eV}=\dfrac{m_Z^2}{2m_\nu}=4.2\cdot \left(\dfrac{eV}{m_\nu}\right)\cdot 10^{21}eV=42\left(\dfrac{0.1eV}{m_\nu}\right)\cdot 10^{21}eV}$

$\boxed{E_{ZeV}=4.2\left(\dfrac{eV}{m_\nu}\right)ZeV=42\left(\dfrac{0.1eV}{m_\nu}\right)ZeV}$

In fact, this mechanism based on “neutral resonances” is completely “universal”! Nothing (except some hidden symmetry or similar) can allow the production of (neutral) particles using this cosmic method. For instance, if this argument is true, beyond the Z-burst, we should be able to detect Higgs-dips (Higgs-bursts) or H-dips, since, similarely we could have

$\nu_{UHE}+\bar{\nu}_{C\nu B}\longrightarrow H\longrightarrow \mbox{hadrons}$

or more generally, with some (likely) “dark” particle, we should also expect that

$\nu_{UHE}+\bar{\nu}_{C\nu B}\longrightarrow X\longrightarrow \mbox{hadrons}$

In the H-dip case, taking the measured Higgs mass from the last LHC run (about 126GeV), we get

$\boxed{E_{eV}(H-dip)=\dfrac{m_H^2}{2m_\nu}=7.9\left(\dfrac{eV}{m_\nu}\right)\cdot 10^{21}eV=79\left(\dfrac{0.1eV}{m_\nu}\right)\cdot 10^{21}eV}$

$\boxed{E_{ZeV}(H-dip)=7.9\left(\dfrac{eV}{m_\nu}\right)ZeV=79\left(\dfrac{0.1eV}{m_\nu}\right)ZeV}$

In the arbitrary “dark” or “weakly interacting” particle, we have (in general, with $m_X= x GeV$ ) the formulae:

$\boxed{E_{eV}(X-dip)=\dfrac{m_X^2}{2m_\nu}=\dfrac{(x GeV)^2}{2m_\nu}=\left(\dfrac{x^2}{2m_\nu}\right)\cdot 10^{18}eV^2=\left(\dfrac{x^2}{2000}\right)\left(\dfrac{1eV}{m_\nu}\right) 10^{21}eV}$

or equivalently

$\boxed{E_{ZeV}(X-dip)=\dfrac{m_X^2}{2m_\nu}=\left(\dfrac{x^2}{200}\right)\left(\dfrac{0.1eV}{m_\nu}\right) ZeV=\left(\dfrac{x^2}{2000}\right)\left(\dfrac{1eV}{m_\nu}\right) ZeV}$

Therefore, cosmic ray neutrino spectroscopy is a very interesting subject yet to come! It can provide:

1st. Evidences for relic neutrinos we expect from the standard cosmological model.

2nd. Evidence for the Higgs boson in astrophysical scenarios from cosmological neutrinos. Now, we know that the Higgs field and the Higgs particle do exist, so it is natural to seek out this H-dips as well!

3rd. Evidence for the additional neutral weakly interacting (and/or “dark”) particles from “unexpected” dips at ZeV (1ZeV=1Zetta electron-volt) or even higher energies! Of course, this is the most interesting part from the viewpoint of new physics searches!

Neutrino telescopes and their associated Astronomy is just rising now! IceCube is its most prominent example…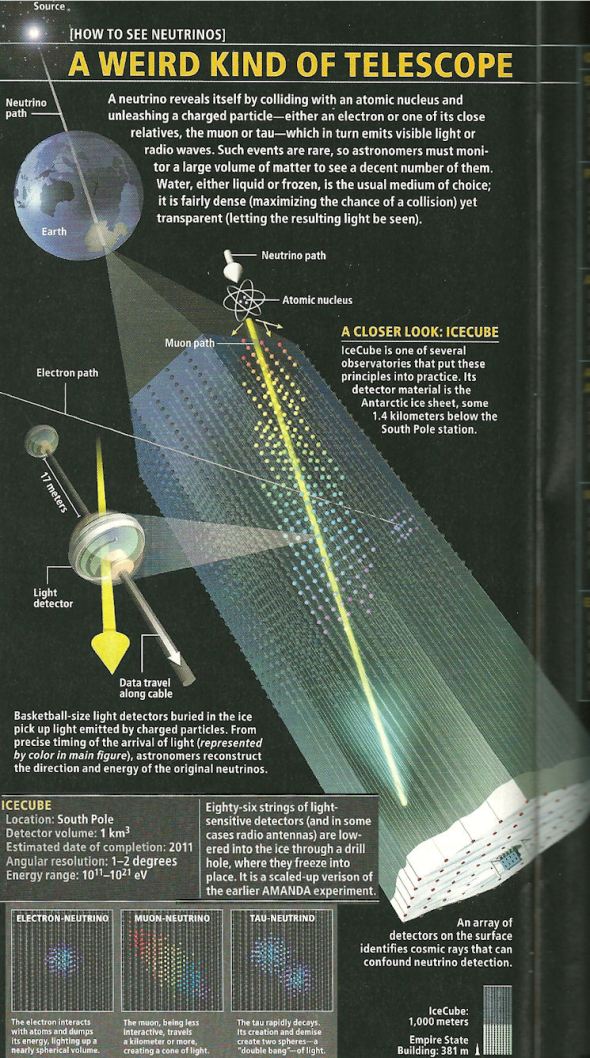

Moreover, following one of the most interesting things in any research (expect the unexpected and try to explain it!) from the scientific viewpoint, I am quite sure the neutrino astronomy and its interplay with cosmic rays or this class of “neutrino spectroscopy” in the flux of cosmic rays open a very interesting window for the upcoming new physics. Are we ready for it? Maybe…After all, the neutrino mixing parameters are very different (“complementary”?) to the quark mixing parameters. You can observe it in this mass-flavor content plot:

Neutrino oscillations are a purely quantum effect, and thus, they open a really interesting “new channel” in which we can observe the whole Universe. Yes, neutrinos are cool!!! The coolest particles in all over the world! We can not imagine yet what neutrino will show and teach us about the current, past and future of the cosmological evolution.

Remark: When I saw the Fermi line and the claim of the Dark Matter particle “evidence” at about 130 GeV, I wondered if it could be, indeed, a hint of a similar “resonant” process in gamma rays, something like

$\gamma \gamma\longrightarrow H (resonance)$

since the line “peaked” close to the known Higgs-like particle mass ( $126GeV\sim 130GeV$ ). Anyway, this line is controversial and its presence has yet to be proved with enough statistical confidence (5 sigmas are usually required in the particle physics community). Of course, the issue with this resonant hypothesis would be that we should expect that this particle would decay into hadrons leaving some indirect clues of those events. The Fermi line can indeed have more explanations and/or be a fluke in the data due to a bad modeling or a bad substraction of the background. Time will tell us if the Fermi line is really here as well.

Final (geek) remark: I wonder if the Doctor Who fans remember that the reality bomb of Davros and the Daleks used “Z-neutrinos“!!! I presently do not know if the people who wrote those scripts and imagined the Z-neutrino were aware of the Z-bursts…Or not… LOL The Z-neutrino powered crucible was really interesting…

And the reality bomb concept was really scaring…

However, neutrinos are pretty weakly interacting particles, at least when they have low energy, so we should have not fear them. After all, their future applications will surprise us much more. I am quite sure of it!

See you in my next neutrinological post!

May the Z(X)-burst induced superGZK neutrinos be with you!

claimtoken-51ead3d045a40

LOG#124. Basic Neutrinology(IX).

Posted: 2013/07/15 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: baryogenesis, baryon to entropy density ratio, baryon-antibaryon asymmetry, entropy ratio, hybrid inflation, inflationary phase, inflationary scenarios, inflaton, left-handed neutrinos, leptogenesis, lepton-antilepton asymmetry, LR models, neutrino masses, neutrinology, non-perturbative effects, Pati-Salam group, reheating, right-handed neutrinos, solar neutrino problem, sphaleron, superfields, SUSY | Leave a comment

In supersymmetric LR models, inflation, baryogenesis (and/or leptogenesis) and neutrino oscillations can be closely related to each other. Baryosynthesis in GUTs is, in general, inconsistent with inflationary scenarios. The exponential expansion during the inflationary phase will wash out any baryon asymmetry generated previously by any GUT scale in your theory. One argument against this feature is the next idea: you can indeed generate the baryon or lepton asymmetry during the process of reheating at the end of inflation. This is a quite non-trivial mechanism. In this case, the physics of the “fundamental” scalar field that drives inflation, the so-called inflaton, would have to violate the CP symmetry, just as we know that weak interactions do! The challenge of any baryosynthesis model is to predict the observed asymmetry. It is generally written as a baryon to photon (in fact, a number of entropy) ratio. Tha baryon asymmetry is defined as

$\dfrac{n_B}{s}\equiv \dfrac{(n_b-n_{\bar{b}})}{s}$

At present time, there is only matter and only a very tiny (if any) amount of antimatter, and then $n_{\bar{b}}\sim 0$ . The entropy density s is completely dominated by the contribution of relativistic particles so it is proportional to the photon number density. This number is calculated from CMBR measurements, and it shows to be about $s=7.05n_\gamma$ . Thus,

$\dfrac{n_B}{s}\propto \dfrac{n_b}{n_\gamma}$

From BBN, we know that

$\dfrac{n_B}{n_\gamma}=(5.1\pm 0.3)\cdot 10^{-10}$

and

$\dfrac{n_B}{s}=(7.2\pm 0.4)\cdot 10^{-11}$

This value allows to obtain the observed lepton asymmetry ratio with analogue reasoning.

By the other hand, it has been shown that the “hybrid inflation” scenarios can be successfully realized in certain SUSY LR models with gauge groups

$G_{SUSY}\supset G_{PS}=SU(4)_c\times SU(2)_L\times SU(2)_R$

after SUSY symmetry breaking. This group is sometimes called the Pati-Salam group. The inflaton sector of this model is formed by two complex scalar fields $H,\theta$ . At the end of the inflation do oscillate close to the SUSY minimum and respectively, they decay into a part of right-handed sneutrinos $\nu_i^c$ and neutrinos. Moreover, a primordial lepton asymmetry is generated by the decay of the superfield $\nu_2^c$ emerging as the decay product of the inflaton field. The superfield $\nu_2^c$ also decays into electroweak Higgs particles and (anti)lepton superfields. This lepton asymmetry is partially converted into baryon asymmetry by some non-perturbative sphalerons!

Remark: (Sphalerons). From the wikipedia entry we read that a sphaleron (Greek: σφαλερός “weak, dangerous”) is a static (time independent) solution to the electroweak field equations of the SM of particle physics, and it is involved in processes that violate baryon and lepton number.Such processes cannot be represented by Feynman graphs, and are therefore called non-perturbative effects in the electroweak theory (untested prediction right now). Geometrically, a sphaleron is simply a saddle point of the electroweak potential energy (in the infinite dimensional field space), much like the saddle point of the surface $z(x,y)=x^2-y^2$ in three dimensional analytic geometry. In the standard model, processes violating baryon number convert three baryons to three antileptons, and related processes. This violates conservation of baryon number and lepton number, but the difference B-L is conserved. In fact, a sphaleron may convert baryons to anti-leptons and anti-baryons to leptons, and hence a quark may be converted to 2 anti-quarks and an anti-lepton, and an anti-quark may be converted to 2 quarks and a lepton. A sphaleron is similar to the midpoint( $\tau=0$ ) of the instanton , so it is non-perturbative . This means that under normal conditions sphalerons are unobservably rare. However, they would have been more common at the higher temperatures of the early Universe.

The resulting lepton asymmetry can be written as a function of a number of parameters among them the neutrino masses and the mixing angles, and finally, this result can be compared with the observational constraints above in baryon asymmetry. However, this topic is highly non-trivial. It is not trivial that solutions satisfying the constraints above and other physical requirements can be found with natural values of the model parameters. In particular, it is shown that the value of the neutrino masses and the neutrino mixing angles which predict sensible values for the baryon or lepton asymmetry turn out to be also consistent with values require to solve the solar neutrino problem we have mentioned in this thread.

LOG#123. Basic Neutrinology(VIII).

Posted: 2013/07/15 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: CDM, CMB, CNB, cold dark matter, cosmic neutrino background, cosmological constant, critical density, HDM, hot dark matter, matter density, neutrino astronomy, neutrino comoslogy, neutrino decoupling, neutrino mass bounds from cosmology, neutrinology, number of effective neutrino species, PLANCK, total matter density, Tremaine-Gunn limit, WMAP | Leave a comment

There are some indirect constraints/bounds on neutrino masses provided by Cosmology. The most important is the one coming from the demand that the energy density of the neutrinos should not be too high, otherwise the Universe would collapse and it does not happen, apparently…

Firstly, stable neutrinos with low masses (about $m_\nu\leq 1 MeV$ ) make a contribution to the total energy density of the Universe given by:

$\rho_\nu=m_{tot}n_\nu$

and where the total mass is defined to be the quantity

$\displaystyle{m_{tot}=\sum_\nu \dfrac{g_\nu}{2}m_\nu}$

Here, the number of degrees of freedom $g_\nu=4(2)$ for Dirac (Majorana) neutrinos in the framework of the Standard Model. The number density of the neutrino sea is revealed to be related to the photon number density by entropy conservation (entropy conservation is the key of this important cosmological result!) in the adiabatic expansion of the Universe:

$n_\nu=\dfrac{3}{11}n_\gamma$

From this, we can derive the relationship of the cosmic relic neutrino background (neutrinos coming from the Big Bang radiation when they lost the thermal equilibrium with photons!) or $C\nu B$ and the cosmic microwave background (CMB):

$T_{C\nu B}=\left(\dfrac{3}{11}\right)^{1/3}T_{CMB}$

From the CMB radiation measurements we can obtain the value

$n_\nu=411(photons)cm^{-3}$

for a perfect Planck blackbody spectrum with temperature

$T_{CMB}=2.725\pm0.001 K\approx 2.35\cdot 10^{-4}eV$

This CMB temperature implies that the $C\nu B$ temperature should be about

$T_{C\nu B}^{theo}=1.95K\approx 0.17meV$

Remark: if you do change the number of neutrino degrees of freedom you also change the temperature of the $C\nu B$ and the quantity of neutrino “hot dark matter” present in the Universe!

Moreover, the neutrino density $\Omega_\nu$ is related to the total neutrino density and the critical density as follows:

$\Omega_\nu=\dfrac{\rho_\nu}{\rho_c}$

and where the critical density is about

$\rho_c=\dfrac{3H_0^2}{8\pi G_N}$

When neutrinos “decouple” from the primordial plasma and they loose the thermal equilibrium, we have $m_\nu>>T$ , and then we get

$\Omega_\nu h^2=10^{-2}m_{tot}eV$

with $h$ the reduced Hubble constant. Recent analysis provide $h\approx 67-71\cdot 10^{-2}$ (PLANCK/WMAP).

There is another useful requirement for the neutrino density in Cosmology. It comes from the requirements of the BBN (Big Bang Nucleosynthesis). I talked about this in my Cosmology thread. Galactic structure and large scale observations also increase evidence that the matter density is:

$\Omega_Mh^2\approx 0.05-0.2$

These values are obtained through the use of the luminosity-density relations, galactic rotation curves and the observation of large scale flows. Here, the $\Omega_M$ is the total mass density of the Universe as a fraction of the critical density $\rho_c$ . This $\Omega_M$ includes radiation (photons), bayrons and non-baryonic “cold dark matter” (CDM) and “hot dark matter” (HDM). The two first components in the decomposition of $\Omega_M$

$\Omega_M=\Omega_r+\Omega_b+\Omega_{nb}+\Omega_{HDM}+\Omega_{CDM}$

are rather well known. The photon density is

$\Omega_rh^2=\Omega_\gamma h^2=2.471\cdot 10^{-5}$

The deuterium abundance can be extracted from the BBN predictions and compared with the deuterium abundances in the stellar medium (i.e. at stars!). It shows that:

$0.017\leq\Omega_Bh^2\leq 0.021$

The HDM component is formed by relativistic long-lived particles with masses less than about $1keV$ . In the SM framework, the only HDM component are the neutrinos!

The simulations of structure formation made with (super)computers fit the observations ONLY when one has about 20% of HDM plus 80% of CDM. A stunning surprise certainly! Some of the best fits correspond to neutrinos with a total mass about 4.7eV, well above the current limit of neutrino mass bounds. We can evade this apparent contradiction if we suppose that there are some sterile neutrinos out there. However, the last cosmological data by PLANCK have decreased the enthusiasm by this alternative. The apparent conflict between theoretical cosmology and observational cosmology can be caused by both unprecise measurements or our misunderstanding of fundamental particle physics. Anyway observations of distant objects (with high redshift) favor a large cosmological constant instead of Hot Dark Matter hypothesis. Therefore, we are forced to conclude that the HDM of $\Omega_M$ does not exceed even $0.2$ . Requiring that $\Omega_\nu <\Omega_M$ , we get that $\Omega_\nu h^2\leq 0.1$ . Using the relationship with the total mass density, we can deduce that the total neutrino mass (or HDM in the SM) is about

$m_\nu\leq 8-10 eV$ or less!

Mass limits, in this case lower limits, for heavy or superheavy neutrinos ( $M_N\sim 1GeV$ or higher) can also be obtained along the same reasoning. The puzzle gets very different if the neutrinos were “unstable” particles. One gets then joint bounds on mass and timelife, and from them, we deduce limits that can overcome the previously seen limits (above).

There is another interesting limit to the density of neutrinos (or weakly interacting dark matter in general) that comes from the amount of accumulated “density” in the halos of astronomical objects. This is called the Tremaine-Gunn limit. Up to numerical prefactors, and with the simplest case where the halo is a singular isothermal sphere with $\rho\propto r^{-2}$ ^, the reader can easily check that

$\rho=\dfrac{\sigma^2}{2\pi G_Nr^2}$

Imposing the phase space bound at radius r then gives the lower bound

$m_\nu>(2\pi)^{-5/8}\left(G_Nh_P^3\sigma r^2\right)^{-1/4}$

This bound yields $m_\nu\geq 33eV$ . This is the Tremaine-Gunn bound. It is based on the idea that neutrinos form an important part of the galactic bulges and it uses the phase-space restriction from the Fermi-Dirac distribution to get the lower limit on the neutrino mass. I urge you to consult the literature or google to gather more information about this tool and its reliability.

Remark: The singular isothermal sphere is probably a good model where the rotation curve produced by the dark matter halo is flat, but certainly breaks down at small radius. Because the neutrino mass bound is stronger for smaller $\sigma r^2$ , the uncertainty in the halo core radius (interior to which the mass density saturates) limits the reliability of this neutrino mass bound. However, some authors take it seriously! As Feynman used to say, everything depends on the prejudges you have!

The abundance of additional weakly interacting light particles, such as a light sterile neutrino $\nu_s$ or additional relativistic degrees of freedom uncharged under the Standard Model can change the number of relativistic degrees of freedom $g_\nu$ . Sometimes you will hear about the number $N_{eff}$ . Planck data, recently released, have decreased the hopes than we would be finding some additional relativistic degree of freedom that could mimic neutrinos. It is also constrained by the BBN and the deuterium abundances we measured from astrophysical objects. Any sterile neutrino or extra relativistic degree of freedom would enter into equilibrium with the active neutrinos via neutrino oscillations! A limit on the mass differences and mixing angle with another active neutrino of the type

$\Delta m^2\sin^2 2\theta\leq 3\cdot 10^{-6}eV^2$ should be accomplished in principle. From here, it can be deduced that the effective number of neutrino species allowed by neutrino oscillations is in fact a litle higher the the 3 light neutrinos we know from the Z-width bound:

$N_\nu (eff)<3.5-4.5$

PLANCK data suggest indeed that $N_\nu (eff)< 3.3$ . However, systematical uncertainties in the derivation of the BBN make it too unreliable to be taken too seriously and it can eventually be avoided with care.

LOG#122. Basic Neutrinology(VII).

Posted: 2013/07/15 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: anomalies, anomalous terms, beyond SM, BSM, Cabibble angle, family symmetry, Froggatt, gauge anomalies, mass hierarchy, neutrino mass from family symmetry, neutrinology, New Physics, particle physics, quark and lepton complementarity, seesaw mechanism, spontaneous symmetry breaking, SSB, U(1) hidden symmetry, vev | Leave a comment

The observed mass and mixing both in the neutrino and quark cases could be evidence for some interfamily hierarchy hinting that the lepton and quark sectors were, indeed, a result of the existence of a new quantum number related to “family”. We could name this family symmetry as $U(1)_F$ . It was speculated by people like Froggatt long ago. The actual intrafamily hierarchy, i.e., the fact that $m_u>>m_d$ in the quark sector, seem to require one of these symmetries to be anomalous.

A simple model with one family dependent anomalous U(1) beyond the SM was first proposed long ago to produce the given Yukawa coupling and their hierarchies, and the anomalies could be canceled by the Green-Schwarz mechanism which as by-product is able to fix the Weinberg angle as well. Several developments include the models inspired by the $E_6\times E_8$ GUT or the $E_8\times E_8$ heterotic superstring theory. The gauge structure of the model is that of the SM but enlarged by 3 abelian U(1) symmetries and their respective fields, sometimes denoted by $X,Y^{1,2}$ . The first one is anomalous and family independent. Two of these fields, the non-anomalous, have specific dependencies on the 3 chiral families designed to reproduce the Yukawa hierarchies. There are right-handed neutrinos which “trigger” neutrino masses by some special types of seesaw mechanisms.

The 3 symmetries and their fields $X,Y^{1,2}$ are usually spontaneously broken at some high energy scale $M_X$ by stringy effects. It is assumed that 3 fields, $\theta_i$ , with $i=1,2,3$ , develop a non-null vev. These $\theta_i$ fields are singlets under the SM gauge group but not under the abelian symmetries carried by $X, Y^{1,2}$ . Thus, the Yukawa couplings appear as some effective operators after the $U(1)_F$ spontaneous symmetry breaking. In the case of neutrinos, we have the mass lagrangian (at effective level):

$\mathcal{L}_m\sim h_{ij}L_iH_uN_j^c\lambda^{q_i+n_j}+M_N\xi_{ij}N_i^cN_j^c\lambda^{n_i+n_j}$

and where $h_ {ij},\xi_{ij}\sim \mathcal{O}(1)$ . The parameters $\lambda$ determine the mass and mixing hierarchy with the aid of some simple relationships:

$\lambda=\dfrac{\langle \theta\rangle}{M_X}\sim\sin\theta_c$

and where $\theta_c$ is the Cabibblo angle. The $q_i,n_i$ are the $U(1)_F$ charges assigned to the left handed leptons L and the right handed neutrinos N. These couplings generate the following mass matrices for neutrinos:

$m_\nu^D=\mbox{diag}(\lambda^{q_1},\lambda^{q_2},\lambda^{q_3})\hat{h}\mbox{diag}(\lambda^{n_1},\lambda^{n_2},\lambda^{n_3})\langle H_u\rangle$

$M_\nu=\mbox{diag}(\lambda^{n_1},\lambda^{n_2},\lambda^{n_3})\hat{\xi}\mbox{diag}(\lambda^{n_1},\lambda^{n_2},\lambda^{n_3})M_N$

From these matrices, the associated seesaw mechanism gives the formula for light neutrinos:

$m_\nu\approx \dfrac{\langle H_u\rangle^2}{M_X}\mbox{diag}(\lambda^{q_1},\lambda^{q_2},\lambda^{q_3})\hat{h}\hat{\xi}^{-1}\hat{h}^T\mbox{diag}(\lambda^{q_1},\lambda^{q_2},\lambda^{q_3})$

The neutrino mass mixing matrix depends only on the charges we assign to the LH neutrinos due to cancelation of RH neutrino charges and the seesaw mechanism. There is freedom in the assignment of the charges $q_i$ . If the charges of the second and the third generation of leptos are equal (i.e., if $q_2=q_3$ ), then one is lead to a mass matrix with the following structure (or “texture”):

$m_\nu\sim \begin{pmatrix}\lambda^6 & \lambda^3 & \lambda^3\\ \lambda^3 & a & b\\ \lambda^3 & b & c\end{pmatrix}$

and where $a,b,c\sim \mathcal{O}(1)$ . This matrix can be diagonalized in a straightforward fashion by a large $\nu_2-\nu_3$ rotation. It is consistent (more or less), with a large $\mu-\tau$ mixing. In this theory or model, the explanation of the large neutrino mixing angles is reduced to a theory of prefactors in front of powers of the parameters $\lambda$ , related with the vev after the family group spontaneous symmetry breaking!

LOG#121. Basic Neutrinology(VI).

Posted: 2013/07/15 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: 3-brane, bulk, bulk mode, bulk state, extra dimensions, extra space-like dimension, KK resonance, KK state, KK tower, left-handed neutrino, model building, neutrino mass matrix from extra dimensions, neutrinology, non-factorirable metric, Planck scale, Randall-Sundrum model, renormalizability, right-handed neutrino, SM brane, sterile neutrino, submicrometer extra dimension, submillimeter extra dimension | Leave a comment

Models where the space-time is not 3+1 dimensional but higher dimensional (generally D=d+1=4+n dimensional, where n is the number of spacelike extra dimensions) are popular since the beginnings of the 20th century.

The fundamental scale of gravity need not to be the 4D “effective” Planck scale $M_P$ but a new scale $M_f$ (sometimes called $M_D$ ), and it could be as low as $M_f\sim 1-10TeV$ . The observed Planck scale $M_P$ (related to the Newton constant $G_N$ ) is then related to $M_f$ in $D=4+n$ dimensions by a relationship like the next equation:

$\eta^2=\left(\dfrac{M_f}{M_D}\right)^2\sim\dfrac{1}{M_f^2R^n}$

Here, $R$ is the radius of the typical length of the extra dimensions. We can consider an hypertorus $T^n=(S^1)^n=S^1\times \underbrace{\cdots}_{n-times} \times S^1$ for simplicity (but other topologies are also studied in the literature). In fact, the coupling is $M_f/M_P\sim 10^{-16}$ if we choose $M_f\sim 1TeV$ . When we take more than one extra dimension, e.g., taking $n=2$ , the radius R of the extra dimension(s) can be as “large” as 1 millimeter! This fact can be understood as the “proof” that there could be hidden from us “large” extra dimensions. They could be only detected by many, extremely precise, measurements that exist at present or future experiments. However, it also provides a new test of new physics (perhaps fiction science for many physicists) and specially, we could explore the idea of hidden space dimensions and how or why is so feeble with respect to any other fundamental interaction.

According to the SM and the standard gravity framework (General Relativity), every group charged particle is localized on a 3-dimensional hypersurface that we could call “brane” (or SM brane). This brane is embedded in “the bulk” of the higher dimensional Universe (with $n$ extra space-like dimensions). All the particles can be separated into two categories: 1) those who live on the (SM) 3-brane, and 2) those who live “everywhere”, i.e., in “all the bulk” (including both the extra dimensions and our 3-brane where the SM fields only can propagate). The “bulk modes” are (generally speaking) quite “model dependent”, but any coupling between the brane where the SM lives and the bulk modes should be “suppressed” somehow. One alternative is provided by the geometrical factors of “extra dimensions” (like the one written above). Another option is to modify the metric where the fields propagate. This last recipe is the essence of non-factorizable models built by Randall, Sundrum, Shaposhnikov, Rubakov, Pavŝiĉ and many others as early as in the 80’s of the past century. Graviton and its “propagating degrees of freedom” or possible additional neutral states belongs to the second category. Indeed, the observed weakness of gravity in the 3-brane can be understood as a result of the “new space dimensions” in which gravity can live. However, there is no clear signal of extra dimensions until now (circa 2013, July).

The small coupling constant derived from the Planck mass above can also be used in order to explain the smallness of the neutrino masses! The left-handed neutrino $\nu_L$ having weak isospin and hypercharge is thought to reside in the SM brane in this picture. It can get a “naturally samll” Dirac mass through the mixing with some “bulk fermion” (e.g., the right-handed neutrino or any other neutral fermion under the SM gauge group) which can be interpreted as a right-handed neutrino $\nu_R$ :

$\mathcal{L}(m,Dirac)\sim h\eta H\bar{\nu}_L\nu_R$

Here, $H,h$ are the two Higgs doublet fields and the Yukawa coupling, respectively. After spontaneous symmetry breaking, this interaction will generate the Dirac mass term

$m_D=hv\eta\sim 10^{-5}eV$

The right-handed neutrino $\nu_R$ has a hole tower of Kaluza-Klein relatives $\nu_{i,R}$ . The masses of these states are given by

$M_{i,R}=\dfrac{i}{R}$ $i=0,\pm 1,\pm 2,\ldots, \pm \infty$

and the $\nu_L$ couples with all KK state having the same “mixing” mass. Thus, we can write the mass lagrangian as

$\mathcal{L}=\bar{\nu}_LM\nu_R$

with

$\nu_L=(\nu_L,\tilde{\nu}_{1L},\tilde{\nu}_{2L},\ldots)$

$\nu_R=(\nu_{0R},\tilde{\nu}_{1R},\tilde{\nu}_{2R},\ldots)$

Are you afraid of “infinite” neutrino flavors? The resulting neutrino mass matrix M is “an infinite array” with structure:

$\mathbb{M}=\begin{pmatrix}m_D &\sqrt{2}m_D &\sqrt{2}m_D &\ldots &\sqrt{2}m_D &\ldots \\ 0 &1/R &0 &\ldots &0 & \ldots\\ 0 & 0 &2/R & \ldots & 0 &\ldots \\ \ldots & \ldots & \ldots & \ldots & k/R & \ldots\\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots\end{pmatrix}$

The eigenvalues of the matrix $MM^+$ are given by a trascendental equation. In the limit where $m_DR\sim 0$ , or $m_D\sim 0$ , the eigenvalues are $\lambda\sim k/R$ , where $k\in \mathbb{Z}$ and $\lambda=0$ is a double eigenvalue (i.e., it is doubly degenerated). There are other examples with LR symmetry. For instance, $SU(2)_R$ right-handed neutrinos that, living on the SM brane, were additional neutrino species. In these models, it has been showed that the left-handed neutrino is exactly massless whereas the assumed bulk and “sterile” neutrino have a mass related to the size of the extra dimensions. These models produce masses that can be fitted to the expected values $\sim 10^{-3}eV$ coming from estimations at hand with the neutrino oscillation data, but generally, this implies that there should be at least one extra dimension with size in the micrometer range or less!

The main issues that extra dimension models of neutrino masses do have is related to the question of the renormalizability of their interactions. With an infinite number of KK states and/or large extra dimensions, extreme care have to be taken in order to not spoil the SM renormalizability and, at some point, it implies that the KK tower must be truncated at some level. There is no general principle or symmetry that explain this cut-off to my knowledge.

May the neutrinos and the extra dimensions be with you!

See you in my next neutrinological post!

LOG#120. Basic Neutrinology(V).

Posted: 2013/07/15 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: bino, dark matter, Dirac mass term, E(6) group, exceptional group GUT, gauginos, GUT, GUT scale, Higgsino, LR models, LSP, Majorana mass term, MSSM, neutralino, neutrino masses, neutrino mixing, proton decay, proton lifetime, R-parity, R-parity violations, seesaw, sfermion, singlets, sneutrino, soft SUSY breaking terms, string inspired models, superparticle, superpartner, superpotential, SUSY models of neutrino masses, vev, WIMPs, wino, Yukawa coupling, Zinos | Leave a comment

Supersymmetry (SUSY) is one of the most discussed ideas in theoretical physics. I am not discussed its details here (yet, in this blog). However, in this thread, some general features are worth to be told about it. SUSY model generally include a symmetry called R-parity, and its breaking provide an interesting example of how we can generate neutrino masses WITHOUT using a right-handed neutrino at all. The price is simple: we have to add new particles and then we enlarge the Higgs sector. Of course, from a pure phenomenological point, the issue is to discover SUSY! On the theoretical aside, we can discuss any idea that experiments do not exclude. Today, after the last LHC run at 8TeV, we have not found SUSY particles, so the lower bounds of supersymmetric particles have been increased. Which path will Nature follow? SUSY, LR models -via GUTs or some preonic substructure, or something we can not even imagine right now? Only experiment will decide in the end…

In fact, in a generic SUSY model, dut to the Higgs and lepton doublet superfields, we have the same $SU(3)_c\times SU(2)_L\times U(1)_Y$ quantum numbers. We also have in the so-called “superpotential” terms, bilinear or trilinear pieces in the superfields that violate the (global) baryon and lepton number explicitly. Thus, they lead to mas terms for the neutrino but also to proton decays with unacceptable high rates (below the actual lower limit of the proton lifetime, about $10^{33}$ years!). To protect the proton experimental lifetime, we have to introduce BY HAND a new symmetry avoiding the terms that give that “too high” proton decay rate. In SUSY models, this new symmetry is generally played by the R-symmetry I mentioned above, and it is generally introduced in most of the simplest models including SUSY, like the Minimal Supersymmetric Standard Model (MSSM). A general SUSY superpotential can be written in this framework as

(1) $\mathcal{W}'=\lambda{ijk}L_iL_jE_l^c+\lambda'_{ijk}L_iQ_jD_k^c+\lambda''_{ijk}D_i^cD_j^cU_k^c+\epsilon_iL_iH_2$

A less radical solution is to allow for the existence in the superpotential of a bilinear term with structure $\epsilon_3L_3H_2$ . This is the simplest way to realize the idea of generating the neutrino masses without spoiling the current limits of proton decay/lifetime. The bilinear violation of R-parity implied by the $\epsilon_3$ term leads by a minimization condition to a non-zero vacuum expectation value or vev, $v_3$ . In such a model, the $\tau$ neutrino acquire a mass due to the mixing between neutrinos and the neutralinos.The $\nu_e, v_\mu$ neutrinos remain massless in this toy model, and it is supposed that they get masses from the scalar loop corrections. The model is phenomenologically equivalent to a “3 Higgs doublet” model where one of these doublets (the sneutrino) carry a lepton number which is broken spontaneously. The mass matrix for the neutralino-neutrino secto, in a “5×5” matrix display, is:

(2) $\mathbb{M}=\begin{pmatrix}G_{2x2} & Q_{ab}^1 & Q_{ab}^2 & Q_{ab}^3\\ Q_{ab}^{1T} & 0 & -\mu & 0\\ Q_{ab}^{2T} & -\mu & 0 & \epsilon_3\\ Q_{ab}^{3T} & 0 & \epsilon_3 & 0\end{pmatrix}$

and where the matrix $G_{2x2}=\mbox{diag}(M_1, M_2)$ corresponds to the two “gauginos”. The matrix $Q_{ab}$ is a 2×3 matrix and it contains the vevs of the two higgses $H_1,H_2$ plus the sneutrino, i.e., $v_u, v_d, v_3$ respectively. The remaining two rows are the Higgsinos and the tau neutrino. It is necessary to remember that gauginos and Higgsinos are the supersymmetric fermionic partners of the gauge fields and the Higgs fields, respectively.

I should explain a little more the supersymmetric terminology. The neutralino is a hypothetical particle predicted by supersymmetry. There are some neutralinos that are fermions and are electrically neutral, the lightest of which is typically stable. They can be seen as mixtures between binos and winos (the sparticles associated to the b quark and the W boson) and they are generally Majorana particles. Because these particles only interact with the weak vector bosons, they are not directly produced at hadron colliders in copious numbers. They primarily appear as particles in cascade decays of heavier particles (decays that happen in multiple steps) usually originating from colored supersymmetric particles such as squarks or gluinos. In R-parity conserving models, the lightest neutralino is stable and all supersymmetric cascade-decays end up decaying into this particle which leaves the detector unseen and its existence can only be inferred by looking for unbalanced momentum (missing transverse energy) in a detector. As a heavy, stable particle, the lightest neutralino is an excellent candidate to comprise the universe’s cold dark matter. In many models the lightest neutralino can be produced thermally in the hot early Universe and leave approximately the right relic abundance to account for the observed dark matter. A lightest neutralino of roughly $10-10^4$ GeV is the leading weakly interacting massive particle (WIMP) dark matter candidate.

Neutralino dark matter could be observed experimentally in nature either indirectly or directly. In the former case, gamma ray and neutrino telescopes look for evidence of neutralino annihilation in regions of high dark matter density such as the galactic or solar centre. In the latter case, special purpose experiments such as the (now running) Cryogenic Dark Matter Search (CDMS) seek to detect the rare impacts of WIMPs in terrestrial detectors. These experiments have begun to probe interesting supersymmetric parameter space, excluding some models for neutralino dark matter, and upgraded experiments with greater sensitivity are under development.

If we return to the matrix (2) above, we observe that when we diagonalize it, a “seesaw”-like mechanism is again at mork. There, the role of $M_D, M_R$ can be easily recognized. The $\nu_\tau$ mass is provided by

$m_{\nu_\tau}\propto \dfrac{(v_3')^2}{M}$

where $v_3'\equiv \epsilon_3v_d+\mu v_3$ and $M$ is the largest gaugino mass. However, an arbitrary SUSY model produces (unless M is “large” enough) still too large tau neutrino masses! To get a realistic and small (1777 GeV is “small”) tau neutrino mass, we have to assume some kind of “universality” between the “soft SUSY breaking” terms at the GUT scale. This solution is not “natural” but it does the work. In this case, the tau neutrino mass is predicted to be tiny due to cancellations between the two terms which makes negligible the vev $v_3'$ . Thus, (2) can be also written as follows

(3) $\begin{pmatrix}M_1 & 0 & -\frac{1}{2}g'v_d & \frac{1}{2}g'v_u & -\frac{1}{2}g'v_3\\ 0 & M_2 & \frac{1}{2}gv_d & -\frac{1}{2}gv_u & \frac{1}{2}gv_3\\ -\frac{1}{2}g'v_d & \frac{1}{2}gv_d & 0 & -\mu & 0\\ \frac{1}{2}g'v_u& -\frac{1}{2}gv_u& -\mu & 0 & \epsilon_3\\ -\frac{1}{2}g'v_3 & \frac{1}{2}gv_3 & 0 & \epsilon_3 & 0\end{pmatrix}$

We can study now the elementary properties of neutrinos in some elementary superstring inspired models. In some of these models, the effective theory implies a supersymmetric (exceptional group) $E_6$ GUT with matter fields belong to the 27 dimensional representation of the exceptional group $E_6$ plus additional singlet fields. The model contains additional neutral leptons in each generation and the neutral $E_6$ singlets, the gauginos and the Higgsinos. As the previous model, but with a larger number of them, every neutral particle can “mix”, making the undestanding of the neutrino masses quite hard if no additional simplifications or assumptions are done into the theory. In fact, several of these mechanisms have been proposed in the literature to understand the neutrino masses. For instance, a huge neutral mixing mass matris is reduced drastically down to a “3×3” neutrino mass matrix result if we mix $\nu$ and $\nu^c$ with an additional neutral field $T$ whose nature depends on the particular “model building” and “mechanism” we use. In some basis $(\nu, \nu^c,T)$ , the mass matrix can be rewritten

(4) $M=\begin{pmatrix}0 & m_D & 0\\ m_D & 0 & \lambda_2v_R\\ 0 & \lambda_2v_R & \mu\end{pmatrix}$

and where the $\mu$ energy scale is (likely) close to zero. We distinguish two important cases:

1st. R-parity violation.

2nd. R-parity conservation and a “mixing” with the singlet.

In both cases, the sneutrinos, superpartners of $\nu^c$ are assumed to acquire a v.e.v. with energy size $v_R$ . In the first case, the $T$ field corresponds to a gaugino with a Majorana mass $\mu$ than can be produced at two-loops! Usually $\mu\approx 100GeV$ , and if we assume $\lambda v_R\approx 1 TeV$ , then additional dangerous mixing wiht the Higgsinos can be “neglected” and we are lead to a neutrino mass about $m_\nu\sim 0.1eV$ , in agreement with current bounds. The important conclusion here is that we have obtained the smallness of the neutrino mass without any fine tuning of the parameters! Of course, this is quite subjective, but there is no doubt that this class of arguments are compelling to some SUSY defenders!

In the second case, the field $T$ corresponds to one of the $E_6$ singlets. We have to rely on the symmetries that may arise in superstring theory on specific Calabi-Yau spaces to restric the Yukawa couplings till “reasonable” values. If we have $\mu=0$ in the matrix (4) above, we deduce that a massless neutrino and a massive Dirac neutrino can be generated from this structure. If we include a possible Majorana mass term of the sfermion at a scale $\mu\approx 100GeV$ , we get similar values of the neutrino mass as the previous case.

Final remark: mass matrices, as we have studied here, have been proposed without embedding in a supersymmetric or any other deeper theoretical frameworks. In that case, small tree level neutrino masses can be obtained without the use of large scales. That is, the structure of the neutrino mass matrix is quite “model independent” (as the one in the CKM quark mixing) if we “measure it”. Models reducing to the neutrino or quark mass mixing matrices can be obtained with the use of large energy scales OR adding new (likely “dark”) particle species to the SM (not necessarily at very high energy scales!).

LOG#119. Basic Neutrinology(IV).

Posted: 2013/07/14 | Author: amarashiki | Filed under: Basic Neutrinology, Physmatics, The Standard Model: Basics | Tags: GUT, LR models, neutrinology, seesaw mechanism, SO(10) unification, SUSY unification | Leave a comment

A very natural way to generate the known neutrino masses is to minimally extend the SM including additional 2-spinors as RH neutrinos and at the same time extend the non-QCD electroweak SM gauge symmetry group to something like this:

$G(L,R)=SU(2)_L\times SU(2)_R\times U(1)_{B-L}\times P$

The resulting model, initially proposed by Pati and Salam (Phys. Rev. D.10. 275) in 1973-1974. Mohapatra and Pati reviewed it in 1975, here Phys. Rev. D. 11. 2558. It is also reviewed in Unification and Supersymmetry: the frontiers of Quark-Lepton Physics. Springer-Verlag. N.Y.1986. This class of models were first proposed with the goal of seeking a spontaneous origin for parity (P) violations in weak interactions. CP and P are conserved at large energies but at low energies, however, the group $G(L,R)$ breaks down spontaneouly at some scale $M_R$ . Any new physics correction to the SM would be of order

$(M_L/M_R)^2$

and where $M\sim m_W$

If we choose the alternative $M_R>>M_L$ , we obtain only small corrections, compatible with present known physics. We can explain in this case the small quantity of CP violation observed in current experiments and why the neutrino masses are so small, as we will see below a little bit.

The quarks $Q$ and their fields, and the leptons and their fields $L$ , in the LR models transform as doublets under the group $SU(2)_{L,R}$ in a simple way. $(Q_L, L_L)\sim (2,1)$ and $(Q_R,L_R)\sim (1,2)$ . The gauge interactions are symmetric under left-handed and right-handed fermions. Thus, before spontaneous symmetry breaking, weak interactions, as any other interaction, would conserve parity symmetry and would become P-conserving at higher energies.

The breaking of the gauge symmetry is implemented by multiplets of LR symmetric Higgs fields. The concrete selection of these multiplets is NOT unique. It has been shown that in order to understand the smallness of the neutrino masses, it is convenient to choose respectively one doublet and two triplets in the following way:

$\phi\sim (2,2,0)$ $\Delta_L\sim (3,1,2)$ $\Delta_R\sim (1,3,2)$

The Yukawa couplings of these Higgs fields with the quarks and leptons are give by the lagrangian term

$\mathcal{L}_Y=h_1\bar{L}_L\phi L_R+h_2\bar{L}_L\bar{\phi}L_R+h_1'\bar{Q}_L\phi Q_R+h'_2\bar{Q}_L\bar{\phi} Q_R+$

$+f(L_LL_L\Delta_L+L_RL_R\Delta_R)+h.c.$

The gauge symmetry breaking in LR models happens in two steps:

1st. The $SU(2)_R\times U(1)_{B-L}$ is broken down to $U(1)_Y$ by the v.e.v. $\langle \Delta_R^0\rangle=v_R\neq 0$ . It carries both $SU(2)_R$ and $U(1)_{B-L}$ quantum numbers. It gives mass to charged and neutral RH gauge bosons, i.e.,

$M_{W_R}=gv_R$ and $M_{Z'}=\sqrt{2}gv_R/\sqrt{1-\tan^2\theta_W}$

Furthermore, as consequence of the f-term in the lagrangian, above this stage of symmetry breaking also leads to a mass term for the right-handed neutrinos with order about $\sim fv_R$ .

2nd. As we break the SM symmetry by turning on the vev’s for the scalar fields $\phi$

$\langle \phi \rangle=\mbox{diag}(v_\kappa,v'_\kappa)$ with

$v_R>>v'_\kappa>> v_\kappa$

We give masses to the $W_L$ and $Z$ bosons, as well as to quarks or leptons ( $m_e\sim hv_\kappa$ ). At the end of the process of spontaneous symmetry breaking (SSB), the two W bosons of the model will mix, the lowest physical mass eigenstate is identified as the observed W boson. Current experimental limits set the limit to $M_{W_R}>550GeV$ . The LHC has also raised this bound the past year!

In the neutrino sector, the above Yukawa couplings after $SU(2)_L$ breaking by $\langle \phi\rangle\neq 0$ leads to the Dirac masses for the neutrino. The full process leads to the following mass matrix for the $\nu, N$ states in the general neutrino mass matrix

$\mathbb{M}_{\nu,N}=\begin{pmatrix}\sim 0 & hv_\kappa\\ hv_\kappa & fv_R\end{pmatrix}$

corresponding to the lighter and more massive neutrino states after the diagonalization procedure. In fact, the seesaw mechanism implies the eigenvalue

$m_{\nu_e}\approx (hv_\kappa)^2/fv_R$

for the lowest mass, and the eigenvalue

$m_N\approx fv_R$

for the (super)massive neutrino state. Several variants of the basic LR models include the option of having Dirac neutrinos at the expense of enlarging the particle content. The introduction of two new single fermions and a new set of carefully chosen Higgs bosons, allows us to write the $4\times 4$ mass matrix

$\mathbb{M}=\begin{pmatrix} 0 & m_D & 0 & 0\\ m_D & 0 & 0 & fv_R\\ 0 & 0 & 0 & \mu\\ 0 & fv_R & \mu & 0\end{pmatrix}$

This matrix leads to two different Dirac neutrinos, one heavy with mass $m_N\sim fv_R$ and another lighter with mass $m_\nu\sim m_D\mu/fv_R$ . This light four component spinor has the correct weak interaction properties to be identified as the neutrino. A variant of this model can be constructed by addition of singlet quarks and leptons. We can arrange these new particles in order that the Dirac mass of the neutrino vanishes at tree level and/or arises at the one-loop level via $W_L-W_R$ boson mixing!

Left-Right symmetric(LR) models can be embedded in grand unification groups. The simplest GUT model that leads by successive stages of symmetry breaking to LR symmetric models at low energies is $SO(10)$ GUT-based models. An example of LR embedding GUT supersymmetric theory can be even discussed in the context of (super)string-inspired models.

The Spectrum of Riemannium

Physmatics in a nutshell, written and explained by a physmatician. Mobilis in mobili!

WARNING: UPGRADED TSOR website!

LOG#127. Basic Neutrinology(XII).

LOG#126. Basic Neutrinology(XI).

LOG#125. Basic Neutrinology(X).

LOG#124. Basic Neutrinology(IX).

LOG#123. Basic Neutrinology(VIII).

LOG#122. Basic Neutrinology(VII).

LOG#121. Basic Neutrinology(VI).

LOG#120. Basic Neutrinology(V).

LOG#119. Basic Neutrinology(IV).

Search box

3QD 2012 award

Read/Watch me here too:

Latest posts

Blog subjects

Parallel reading

Papers, talks, data

Spanish Sci-blogs

Extrasolar planets

Technology

Useful software

Science for Everyone

Images from the Universe

Friends

Fun

Free e-books and lectures

Blogroll

My Linux

E-learning

Blog Statistics

Meta stuff

Tags

My twitter account

TSOR (Facebook)

amarashiki

Physmatics in a nutshell, written and explained by a physmatician. Mobilis in mobili!

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Search box

3QD 2012 award

Read/Watch me here too:

Latest posts

Blog subjects

Parallel reading

Papers, talks, data

Spanish Sci-blogs

Extrasolar planets

Technology

Useful software

Science for Everyone

Images from the Universe

Friends

Fun

Free e-books and lectures

Blogroll

My Linux

E-learning

Blog Statistics

Meta stuff

Tags

amarashiki